一般而言，非论初中或高中皆不会学习三次方程的求根公式，高考也不会考求解三次方程。

要是初中同学遭遇解三次方程的问题，那么一定是大致的三次方程，存在好意思妙的解法。

举个例子。

题目呈现：

解方程x³+x=130

解题想路：诚然三次方程存在求根公式，然而最佳秘密用公式解方程。初中学习了因式明白，计划把常数项转移到左边，再进行因式明白。

解：x³+x-130=0

x³-5x²+5x²+x-130=0

x²(x-5)+(x-5)(5x+26)=0

(x-5)(x²+5x+26)=0

∴ x=5

三次方程必有一个实数根。为什么呢？因为虚根成对出现，是以三次方程至少有一个实数根。

多项式x²+5x+26无实根，因为判别式Δ

除此以外，还有一种很漂亮的解法。

x³+x=130

x³+x=125+5

x³+x=5³+5

∴ x=5.

这种解法称为同构法。

如何看出方程的一个实数根的？网友称为瞋目法，骨子上是试根法。即以常数项为冲突口，因数明白，130共有1，2，5，13这几个质因数，区别取正负值代入方程覆按找到一个根。

知谈了三次方程的一个根，就不错用多项式除法降次，问题转机为咱们老到的二次方程就好贬责了。

比如说找到一个根x=5，那么x-5势必是多项式的一个因式，作念一次除法如下图所示：

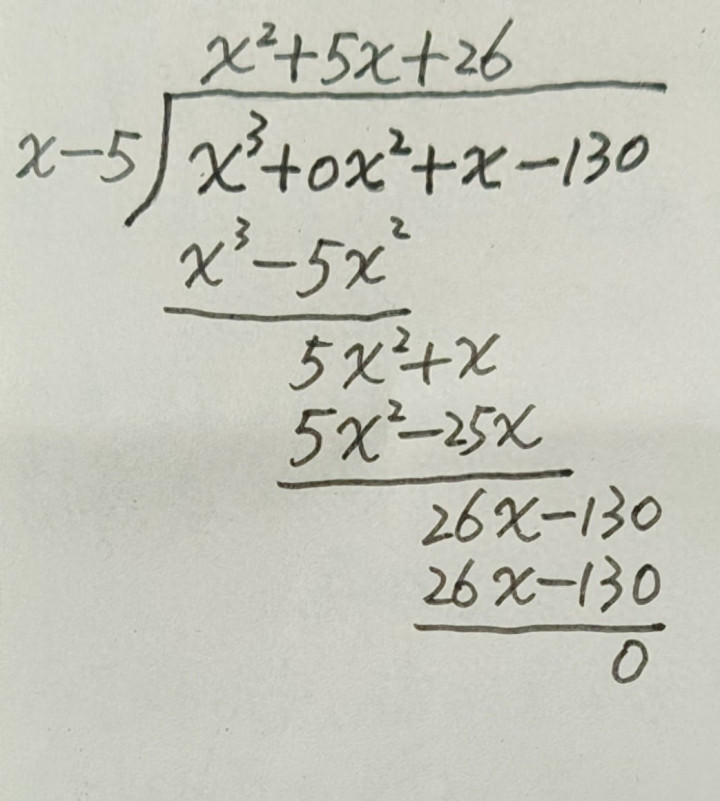
接下来咱们大致了解一下三次方程的解法，图片来自李毓佩训导的册本《代数的威力》截图。

紧接下图

复杂的三次方程举个例子。

意大利数学家卡尔达诺还是向另一位数学家塔尔塔利亚求教过底下的方程的解法：

x³+3x=10

这个方程的数值解是x≈1.6989

这个方程的代数解(根式解)很复杂，咱们不错用数学软件求根，效果如下图所示：

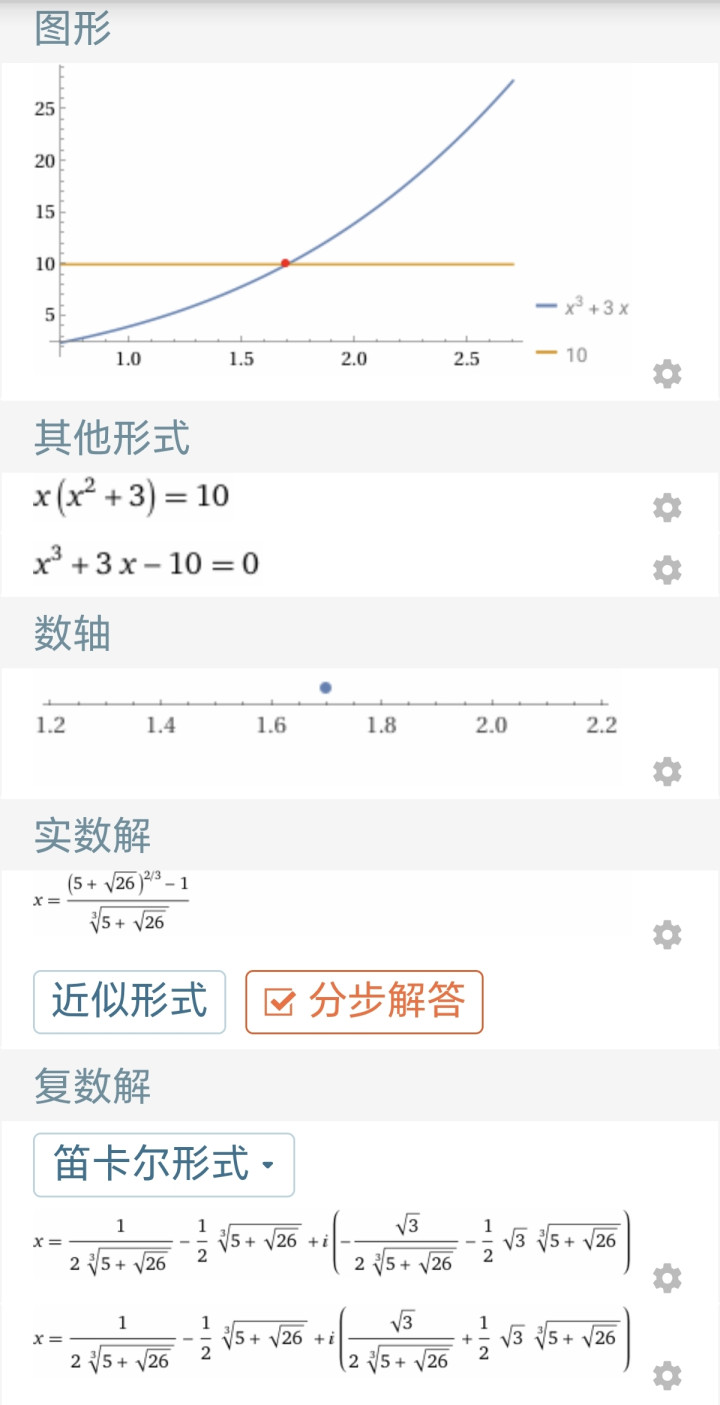
历史受骗先发表三次方程求根公式的数学家是卡尔达诺，他把缺项三次方程的解法写在他的著述《大法》中。书中天然莫妥贴代形势的求根公式，而是用翰墨刻画。

16世纪的这段旧事也证据了一个真理：不发表就发霉。卡尔达诺诚然不是原创，然而抢到了首发，从而青史留名。

科学尚未进步，媒体还需极力。感谢阅读，邂逅。